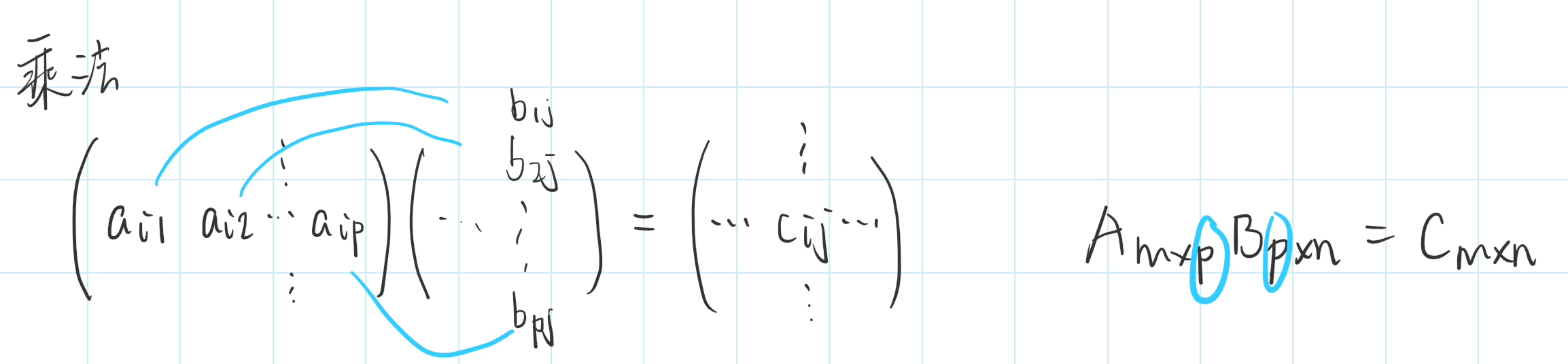线性运算
加法
A=[aij]m×n, B=[bij]m×n, C=A+B=[aij+bij]m×n
数乘
A=[aij]m×n∈F,k∈F,B=kA=[kaij]m×n
非线性运算
乘法
A=[aij]m×p,B=[bij]p×n∈F, 令 cij=ai1b1j+ai2b2j+...+aipbpj
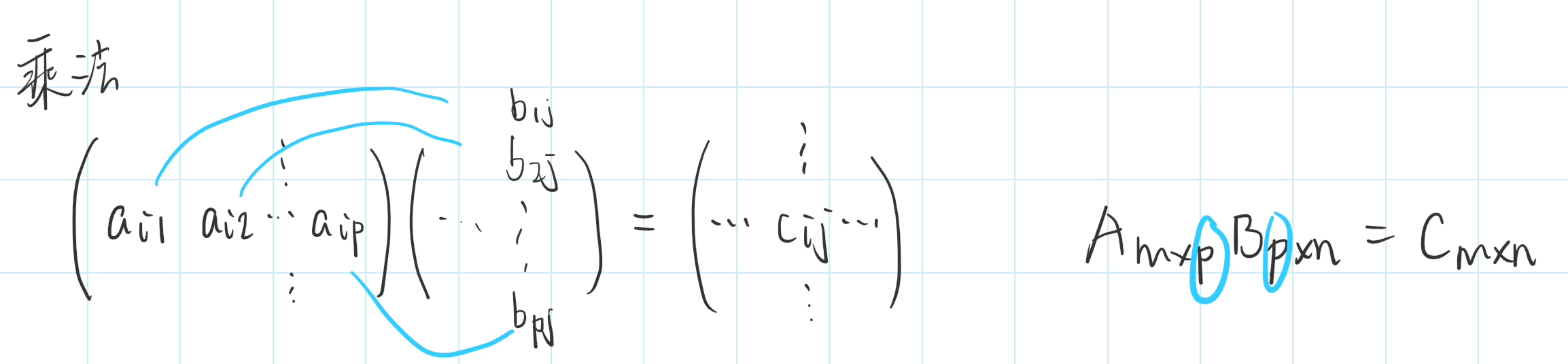
- 不具有交换律 AB=BA
- AB 有意义,BA 不一定有意义
- AB 和 BA 都有意义, 也不一定同型
- AB 和 BA 同型, 也不一定相等
- A=0,B=0 不能导出 AB=0
- AB=AC,A=0 不能导出 B=C
- 乘入方式一致
单位矩阵
斜对角都为 1 的 n×n 矩阵 In (或 I;En或E)
幂运算
A0=I,A1=A
设 A 为方阵, k,l 为非负整数, f(x) 是 x 的一元多项式
- AkA1=Ak+1
- f(x)=g(x)h(x),f(A)=g(A)h(A)
若 f(x)=anxn+an−1xn−1+...+a1x+a0
则 f(A)=anAn+an−1An−1+...+a1A+a0I
- 由于 f(x) 末项为 x0, f(A) 末项为 I
An−I=(A−I)(An−1+An−2+...+A+I)
一般地,
- (AB)k=AkBk
- (A+B)2=A2+2AB+B2
- A2−B2=(A−B)(A+B)
当且仅当 AB=BA 时上述式可取等
设 A 与 B 为同阶矩阵, 若 AB=BA,
(A+B)n=∑k=0nCnkAiBn−k
转置矩阵
Am×n 的转置矩阵为 n×m 矩阵, 记为 AT
- AAT=A
- (A+B)T=AT+BT
- (kA)T=kAT
- (AB)T=BTAT
- (ABC)T=CTBTAT
设 A 与 B 是同阶方阵, 则 ABT+BAT=ABT+BAT
- 对称矩阵: AT=A
- 反称矩阵: AT=−A