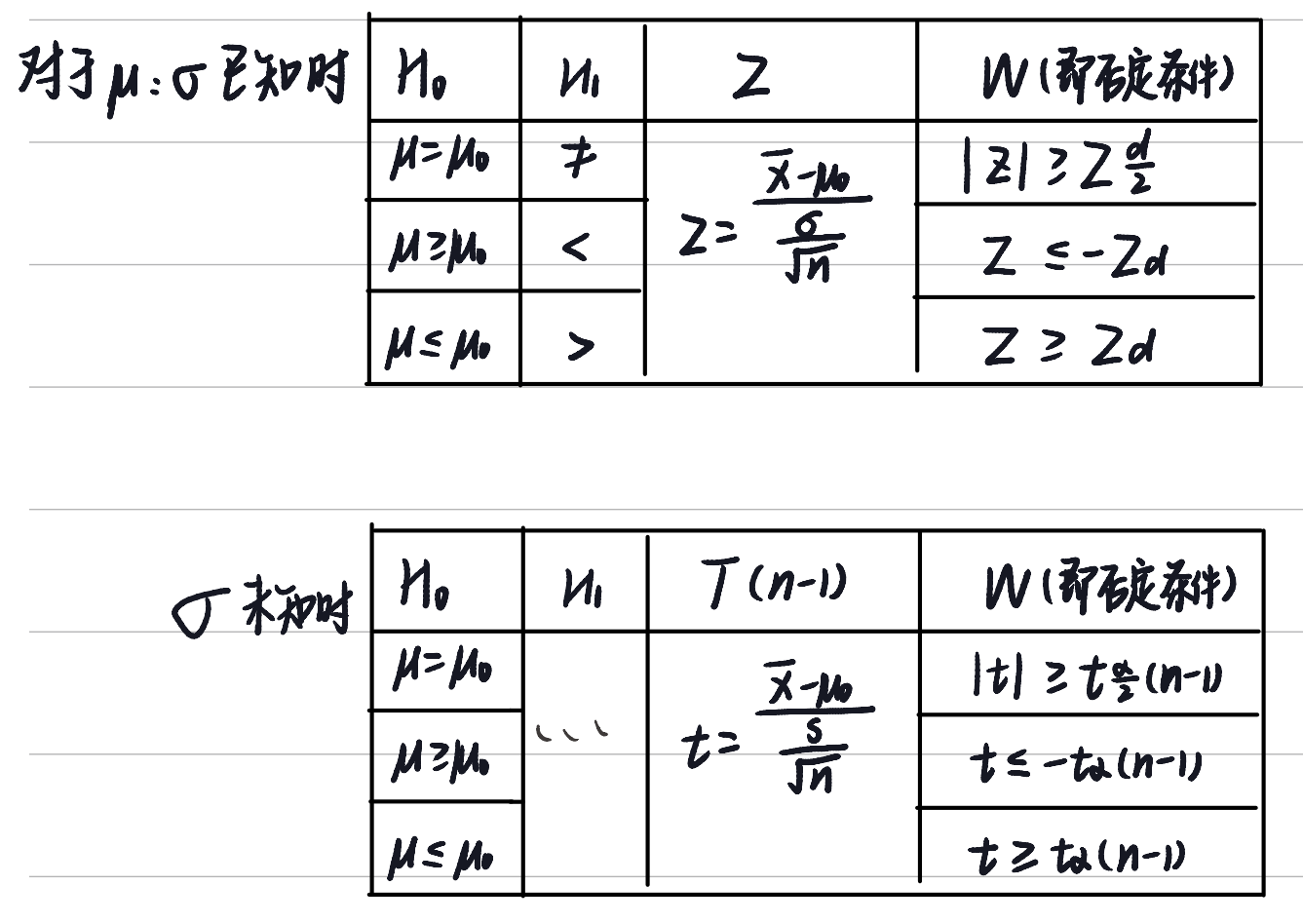
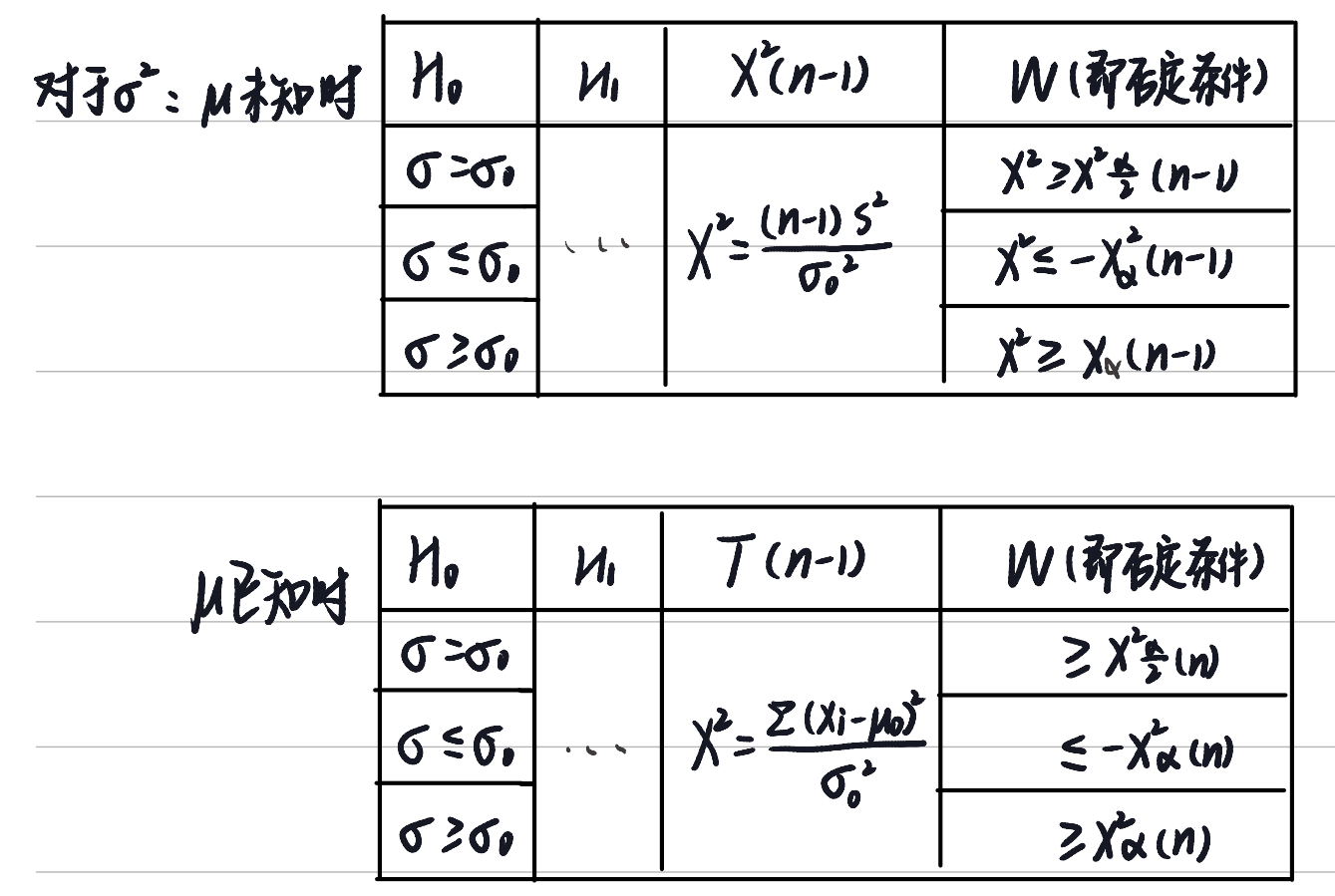
设总体 X∼N(μ,σ2), Xi 为来自总体 X 的样本. 显著水平 为 α, μ0 为已知的常数.
- 当 σ2 已知时, H0:μ=μ0,H1:μ=μ0, 从 μ 的点估计 X 出发构造拒绝域 W={(x1,...,xn):∣x−μ0∣≤C}, 按照控制第一类错误的原则 P{∣X−μ0∣≤C∣H0成立}=α, 根据 抽样分布 定理, σ/nX−μ∼N(0,1), 当 H0:μ=μ0 成立时, Z=σ/nX−μ0∼N(0,1). 查表 zα/2, 计算.
- 当 σ2 已知时, H0:μ≤μ0,H1:μ>μ0, 拒绝域 W={(x1,...,xn):x−μ0≥C1}, 按照控制第一类错误的原则 P{σ/nx−μ0≥C∣H0}≤α, C=σ/nC1. 根据 抽样分布 定理, σ/nX−μ∼N(0,1). 查表得 zα, 计算.
- 当 σ2 已知, H0:μ≥μ0,H1:μ<μ0 时, 检验统计量为 σ/nx−μ0, 拒绝域为 W={(xi):σ/nx−μ0≤−zα}.