建立假设, 先假设符合要求, 即 , 称为原假设或零假设, 记为 , 当原假设 不成立时, 称 的其他取值为备择假设或对立假设, 记为 .
检验统计量
先假定原假设 成立, 根据样本构造一个合适的小概率事件. 如果在一次具体抽样中这个小概率事件发生了, 此时与小概率原理相矛盾, 说明原假设 成立的假定是错误的, 若小概率事件没有发生, 则无法拒绝原假设 .
由于样本所含信息分散, 构建一个统计量进行判断, 称为检验统计量.
指向原始笔记的链接
检验法则
当 时, 拒绝 , 否则接受 .
令 称为检验的拒绝域, 边界点为检验的临界点, 为检验的接受域.
指向原始笔记的链接
显著水平与临界值
当实际 为真时仍有可能做出拒绝的判断, 无法排除这类错误, 因此希望将这种错误的概率控制在一定的限度内, 给出一个较小的数 , 使得 , 其中 称为检验的显著性水平.
指向原始笔记的链接
- 根据问题要求和信息提出原假设 和备择假设 ;
- 构造检验统计量;
- 确定拒绝域的形式;
- 给定显著性水平 的值, 确定临界点 ;
- 根据样本观察值作出是否拒绝 的判断.
第一类错误
原假设 为真, 但由于样本的随机性使得观测值落入拒绝域, 称为第一类错误, 概率称为拒真概率.
指向原始笔记的链接
第二类错误
原假设 为加, 但由于样本的随机性使得观测值落入接受域, 称为第二类错误, 概率称为取伪概率.
指向原始笔记的链接
在一般情形, 样本容量固定时, 减小一类错误概率回导致另一类错误概率的增加.
一般来说, 总是控制犯第一类错误的概率, 使它不大于 , 的大小视具体情况而定, 然后在此约束下根据对犯第二类错误概率的实际要求选取适当的样本容量.
关于均值的假设检验
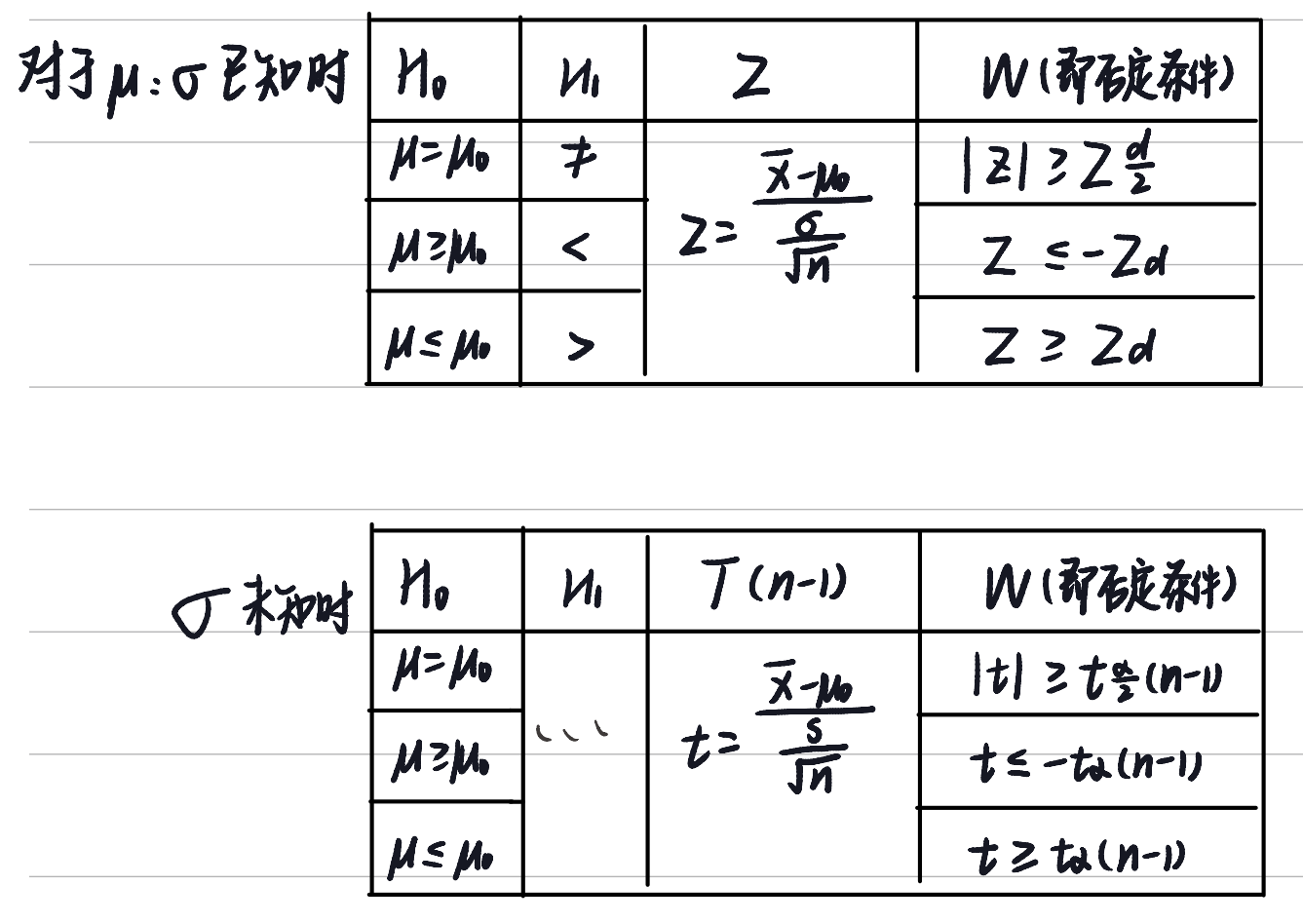
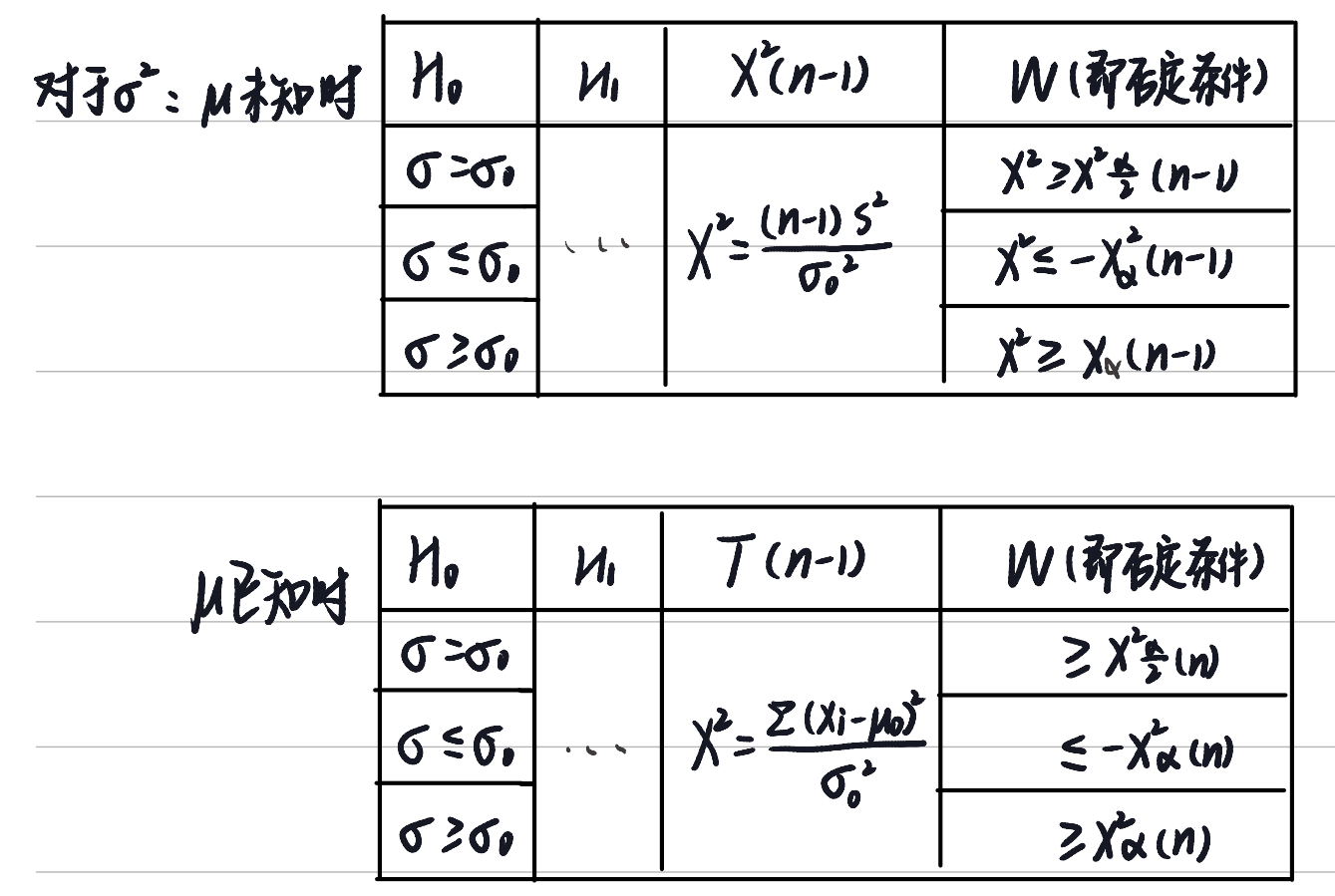
设总体 , 为来自总体 的样本. 显著水平 为 , 为已知的常数.
- 当 已知时, , 从 的点估计 出发构造拒绝域 , 按照控制第一类错误的原则 , 根据 抽样分布 定理, , 当 成立时, . 查表 , 计算.
- 当 已知时, , 拒绝域 , 按照控制第一类错误的原则 , . 根据 抽样分布 定理, . 查表得 , 计算.
- 当 已知, 时, 检验统计量为 , 拒绝域为 .
指向原始笔记的链接